Transversal Line and Angles
LESSON – TRANSVERSAL LINE AND ANGLES
TOPIC
- Introduction
- Parallel Line
- Transversal Line
- Transversal Angles
INTRODUCTION
A line is a straight or curved mark made by marking materials like pen, pencil, etc.
An angle is the space between two intersecting lines.
PARALLEL LINES
Parallel lines are lines in a plane that are always the same distance apart like equal sign.
______________________
______________________
TRANSVERSAL LINES
Transversal line are lines that intersect two straight lines or parallel lines at distinct points.
TRANSVERSAL ANGLES
Transversal angles are angles formed when a straight line cuts the two parallel lines.
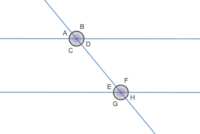
TRANSVERSAL ANGLES
The following are transversal angles,
1. Corresponding angles
2. Alternate Interior Angles
3. Alternate Exterior Angles
4. Opposite Angles
CORRESPONDING ANGLES
Corresponding angles are angles formed in the same position when a line cross the parallel lines.

In the above, all the following are corresponding angles –
- A and E
- C and G
- B and F
- D and H
ALTERNATE ANGLES
Alternate angles are angles that are on the opposite sides of the transversal line.
All alternate angles are equal angles.
There are two (2) types of alternate angles, interior and exterior angles.
The angles formed inside the opposite sides are known are as interior angles. While angles formed outside opposite sides are known as exterior angles.
In the above, the following are alternate interior angles –
- C and F
- D and E
While, the following are alternate exterior angles –
- A and H
- B and G
OPPOSITE ANGLES
Opposite angles are angles that are directly opposite to each on the transversal line.
These angles are equal angles and also known as vertical angles.
The following are vertical or opposite angles,
- A and D
- B and C
- E and H
- F and G
CO – INTERIOR ANGLES
Co – interior angles are angles between two parallel angles.
These are on the same sides of the transversal line.
The sum of the co – interior angles is equal to 180°.

In the above diagram, the following are co – interior angles –
- D and F, D + F = 180°
- C and E, C + E = 180°
SUPPLEMENTARY ANGLES
Supplementary angles are two angles that are sum up to 180º on the transversal line.
Supplementary angles are as follows:
- A and B, A + B = 180º
- A and C
- C and D
- B and D, etc.
WORKING EXAMPLE
If A =46°, find the B, C, D, E, F, G and H.
SOLUTIONS
If A = 46°, A + B = 180 (supplementary angles).
B = 180° – 46° = 134°
- B = C = 134°(opposite angles)
- A = D = 46° (opposite angles)
- A = E = 46° (corresponding angles)
- E = H = 46° (opposite angles)
- B = F = 134° (corresponding angles)
- F = G = 134° (corresponding angles)
Therefore, A = 46°, B = 134°, C = 134°, D =46°, E = 46°, F = 134°, G = 134° and H = 46°.
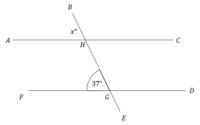
WORKING EXERCISE
Find the letter a – g,
LESSON EVALUATION
Answer 5 questions including number 6.
1. explain the meaning of angle.
2. list and explain types of angles.
3. different between transversal line and transversal angles.
4. draw a transversal line on parallel lines.
5. differentiate between transversal line and parallel lines.
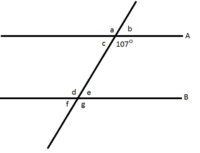
6. Find the following letters,